Any bootstrap model selection procedure is time consuming. However, for linear models, we have leveraged the efficiency of the branch-and-bound algorithm provided by leaps (Lumley & Miller, 2009; Miller, 2002). The bestglm package is used for GLMs; but in the absence of a comparably efficient algorithm the computational burden is much greater (McLeod & Xu, 2014).
Furthermore, we have taken advantage of the embarrassingly parallel nature of bootstrapping, utilising the doParallel and foreach packages to provide cross platform multicore support, available through the cores argument. By default it will detect the number of cores available on your computer and leave one free.
Figure shows the timing results of simulations run for standard use scenarios with 4, 8 or 16 cores used in parallel. Each observation plotted is the average of four runs of a given model size. The simulated models had a sample size of \(n=100\) with \(5,10,\ldots,50\) candidate variables, of which 30% were active in the true model.
The results show both the vis() and af() functions are quite feasible on standard desktop hardware with 4 cores even for moderate dimensions of up to 40 candidate variables. The adaptive fence takes longer than the vis() function, though this is to be expected as the effective number of bootstrap replications is B\(\times\)n.c, where n.c is the number divisions in the grid of the parameter \(c\).
The results for GLMs are far less impressive, even when the maximum dimension of a candidate solution is set to nvmax = 10. In its current implementation, the adaptive fence is only really feasible for models of around 10 predictors and the vis() function for 15. Future improvements could see approximations of the type outlined by to bring the power of the linear model branch-and-bound algorithm to GLMs. An example of how this works in practice is given in Section .
An alternative approach for high dimensional models would be to consider subset selection with convex relaxations as in or combine bootstrap model selection with regularisation. In particular, we have implemented variable inclusion plots and model stability plots for glmnet (Shen et al., 2012). In general, this is very fast for models of moderate dimension, but it does not consider the full model space. Restrictions within the glmnet package, mean it is only applicable to linear models, binomial logistic regression, and Poisson regression with the log link function. The glmnet package also allows for "multinomial", "cox", and "mgaussian" families, though we have not yet incorporated these into the mplot package.
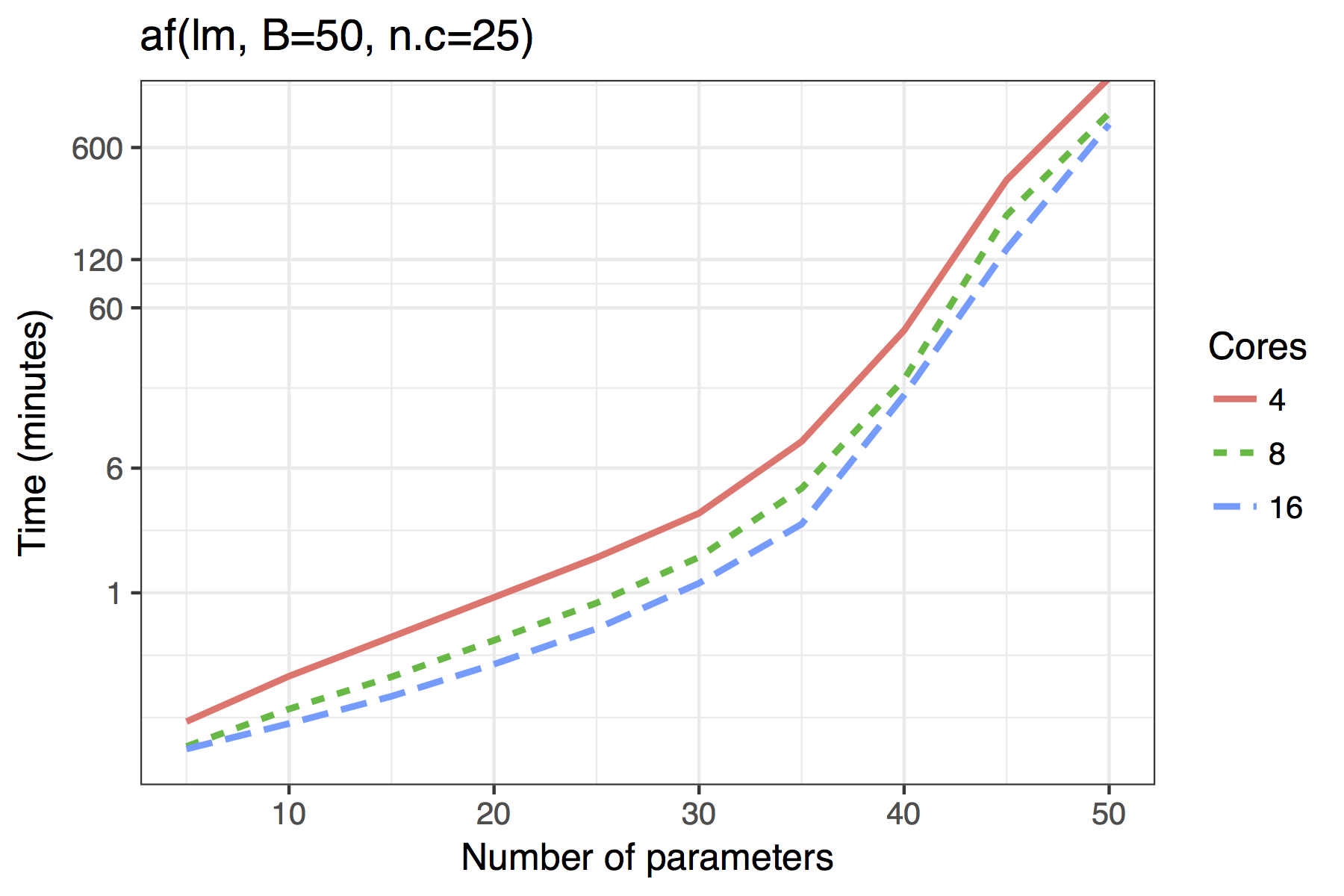
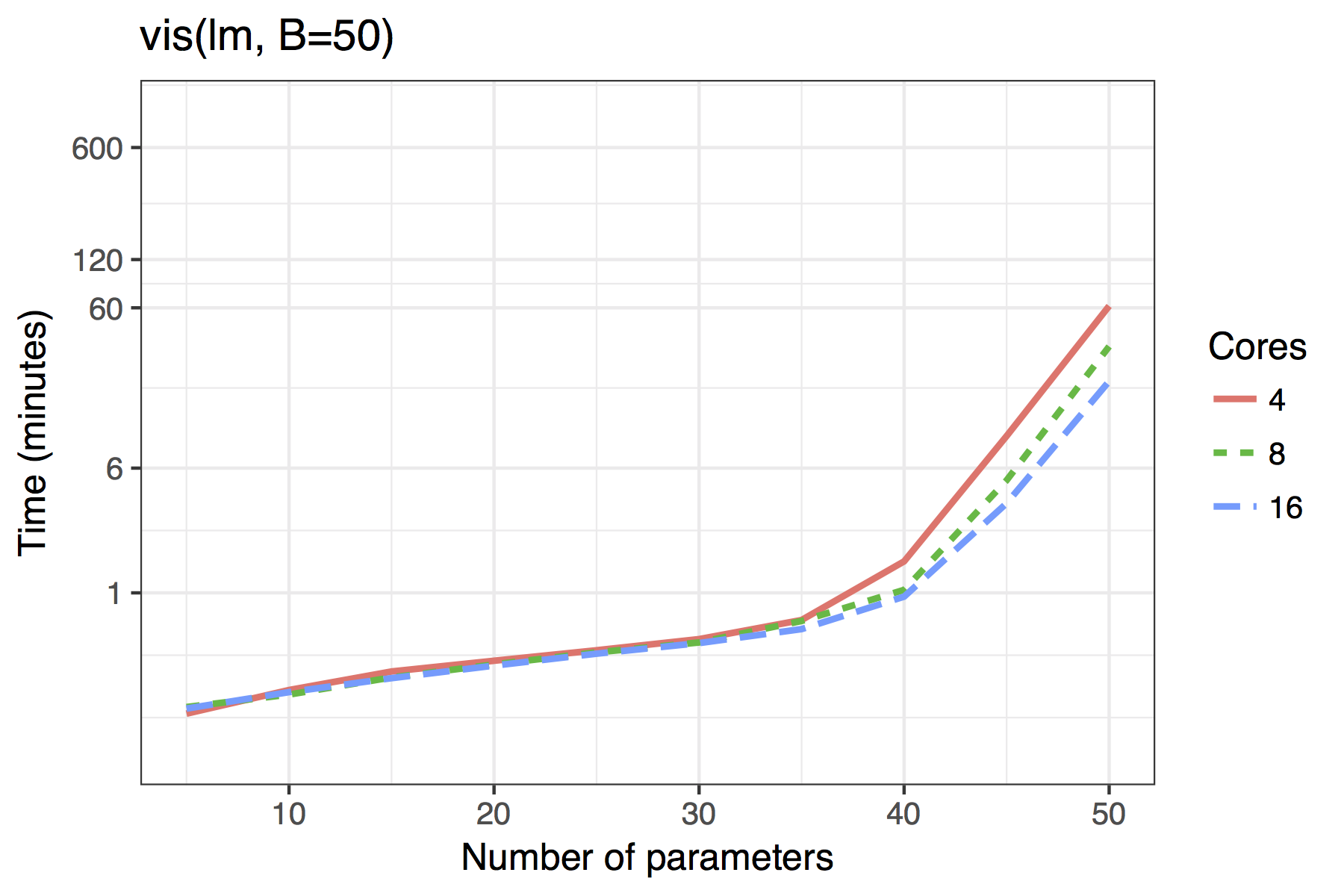
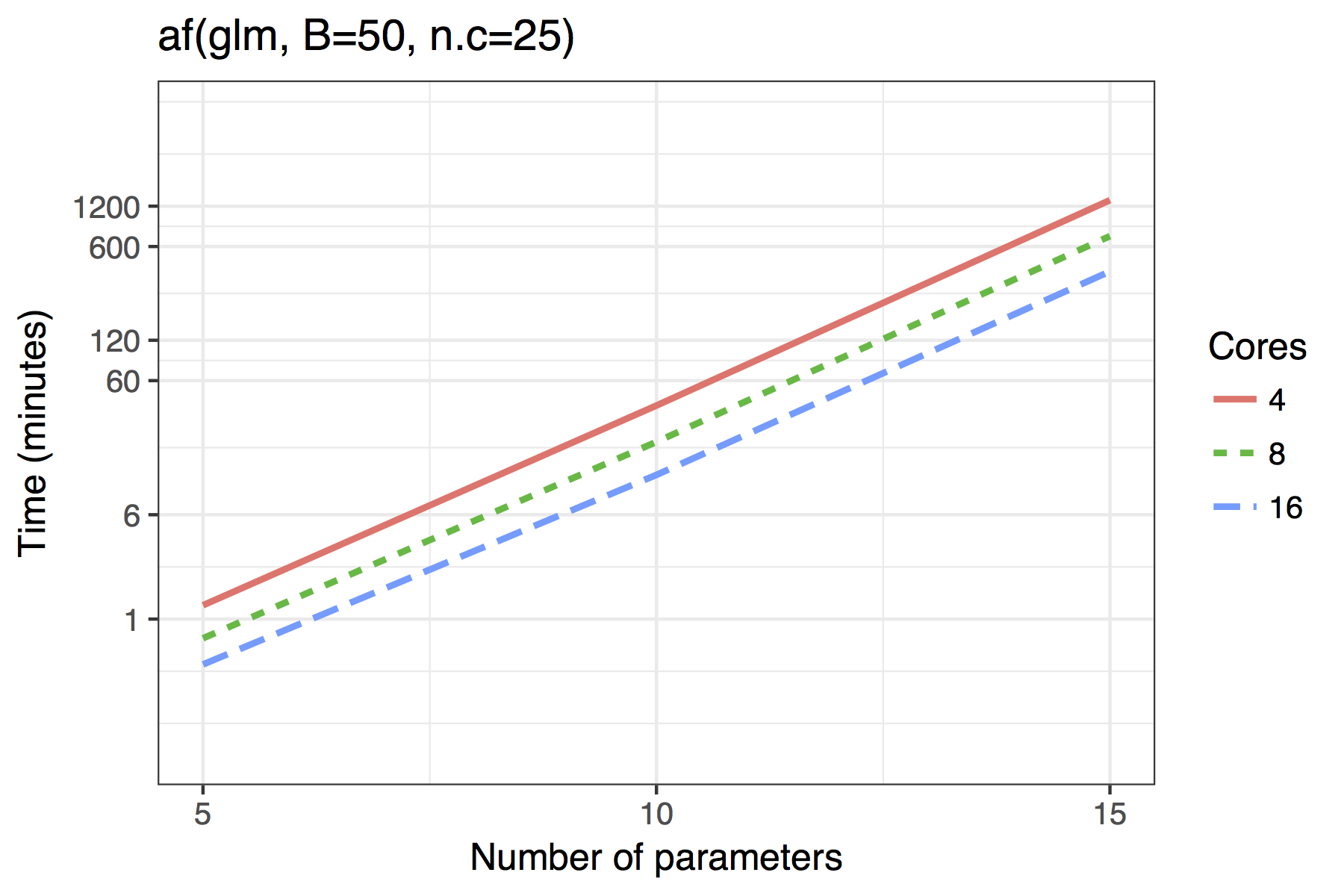
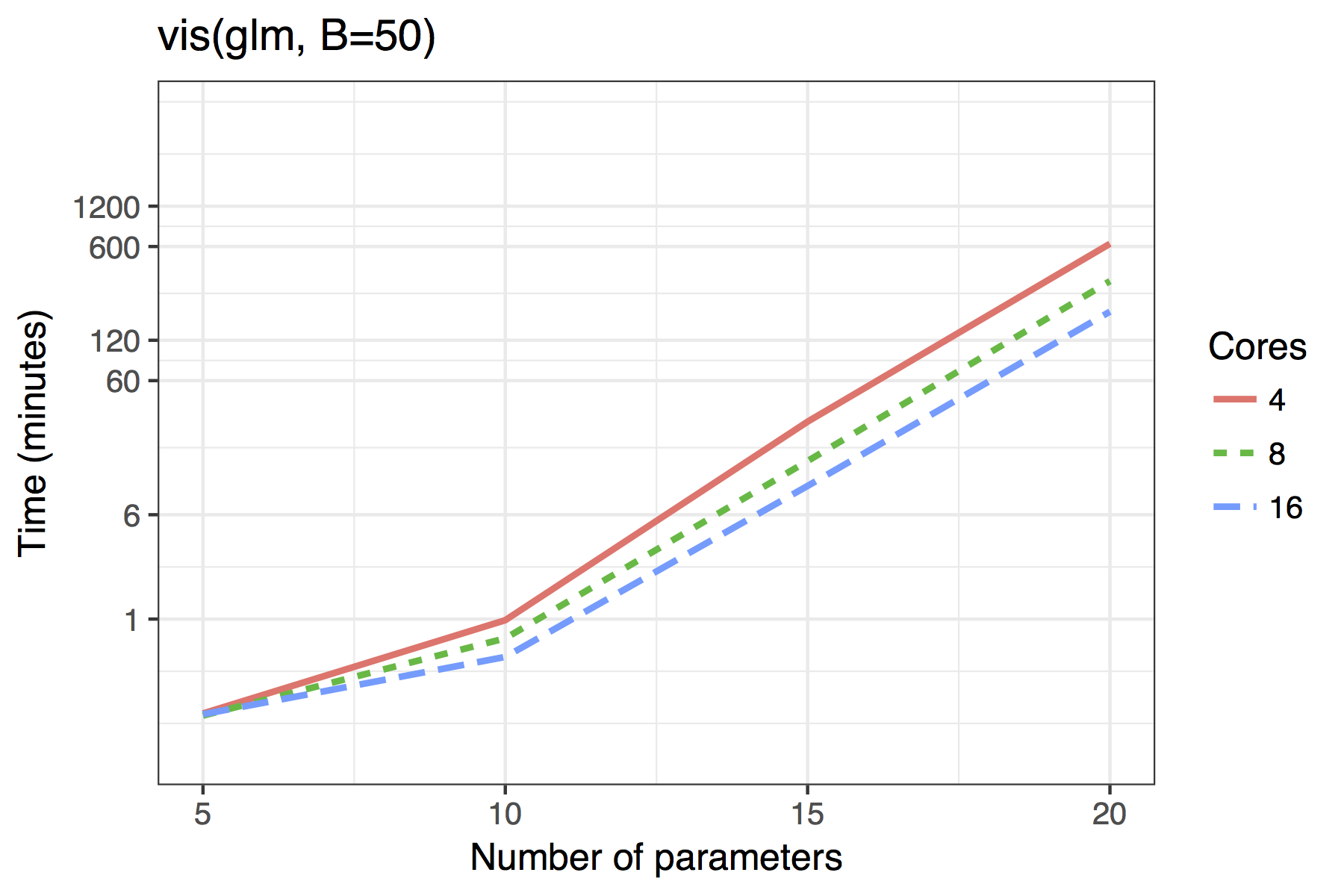
Average time required to run the af() and vis() functions when \(n=100\). A binomial regression was used for the GLM example.